I’m sure many of you know of Han Solo’s famous Kessel Run–which he made in “less than 12 parsecs.”

He says this as if he’s declaring a new time record, like I might brag that I ran a marathon in 2 hours. (I haven’t.)

The problem: parsecs are, in fact, a unit of distance. Not time.

I’ve seen a lot of internet chatter from Star Wars fans, positing ideas as to whether this was a scriptwriting mistake or whether Solo took some kind of distance shortcut. But it’s far from the only astronomical measurement that people get confused.

And why wouldn’t you? After all, the distances–and times, temperatures, masses, etc–that we talk about in astronomy are so huge they boggle the mind.

So let’s break this down…

1. The Metric System
2. Temperatures
3. Astronomical Unit
4. Light-Year
5. Seconds/Minutes/Degrees of Arc
6. Parsecs
7. Solar Units

Let’s start with the basics.

The Metric System

I don’t know about you, but I know I’m way more familiar with imperial than metric.

No, no, not that kind of “Imperial”…I’m a Trekkie!

When you’re brought up with the imperial measurement system, the metric system feels very strange to adjust to. After all, I think in terms of inches, feet, yards, and miles, not centimeters, meters, and kilometers. In my daily life, I don’t have much concept of how long a kilometer is.

(If you’re already familiar with the metric system, you can probably skip right on to the next section!)

The thing with the metric system is that, mathematically speaking, it’s actually way easier to use. Just look at how contrived these imperial conversions are…

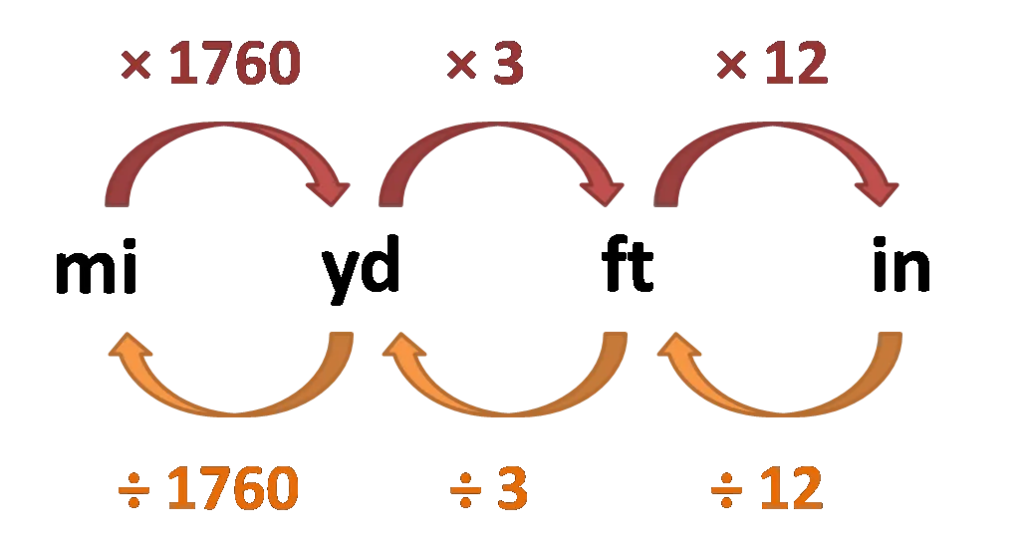
To get from inches to feet, we divide by 12. Easy enough to remember. Then to get to yards, we divide by 3…okay. And then to get to miles, we divide by…

…1760?? What?

This feels so random. I’ve grown up with imperial my whole life, and I’d have to look up that number every time I used it.

Metric, on the other hand…

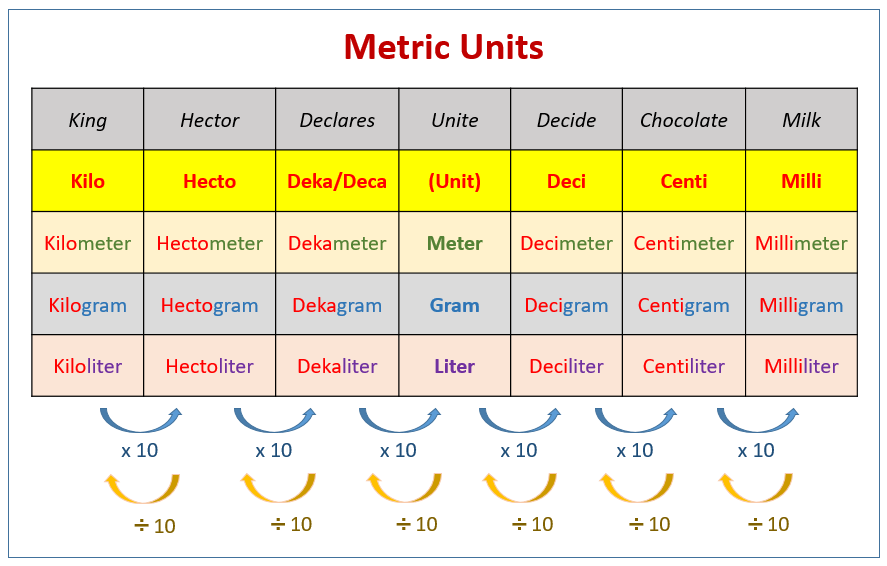
Look how pretty and simple that is. You just multiply or divide by 10 every single time.

The best part of metric is that it follows our existing number system. We use a base 10 system, where each “place” in a number is a multiple or divisor of 10–for example, the tens place, the hundreds place, the thousands place, etc. The metric system compliments this quite nicely.

The metric system is the common name for the International System of Units (SI), and the international standard of measurement. In general, science classes and scientific research stick to SI units.

Got the metric system down? Okay, good. Let’s move on to temperature.

Temperatures

When it comes to temperatures, there’s one unit my fellow Americans are intimately familiar with: Fahrenheit.

Wait, no, not that Fahrenheit…

The Fahrenheit temperature scale isn’t metric, though. Heck, it’s not even imperial! It’s kind of a rebel, doing its own thing. It’s defined based on a fairly arbitrary pair of values: the freezing point of brine, 0°F, and the average human body temperature, originally set at 90ºF.

I don’t know about you, but that sounds downright random.

The metric system gives us Celsius, which uses a much more sensible pair of defining values: the freezing point of water (0°C), and the boiling point of water (100°C).

But even Celsius can only take astronomers so far. The freezing point of water is still an arbitrary number: why water? What makes water special? Why base our entire understanding of all the temperatures in the universe off of the properties of water?

Water is very important on Earth, but it remains a very terrestrial defining value.

Enter, stage left: the Kelvin scale.

The Kelvin scale is an adaptation of the Celsius scale. It was designed for easy conversion: just take a Celsius temperature, add 273.15, and you have kelvins.

Another minor difference: Celsius is expressed in degrees (for example, 10°C), whereas Kelvin is expressed in “kelvins” (for example, 10 kelvins–or the equivalent of 10°C, 283.15 kelvins).

But it has a much more astronomical defining point: absolute zero.

Absolute zero is theoretical. It is the coldest possible temperature, at which no more heat can be removed from a material. Absolute zero is 0 kelvins, so there are no negative numbers on the Kelvin scale.

You’ve likely seen me reference Kelvin all over this blog, usually referring to stellar temperatures (and, recently, the cosmic microwave background radiation).

Celsius and Kelvin are both SI units–but kelvins are definitely more convenient for astronomers.

Alrighty, got kelvins down? Now let’s talk about distances…

Astronomical Unit

The metric system is the standard among scientists. But when astronomers try measuring the distance between the Earth and the sun–let alone larger distances! –they run into a problem.

Just the distance between the Earth and the sun is 92,955,807 million miles, or 149,597,871 kilometers. And that’s not a convenient number to work with at all.

It gets worse–this is practically the smallest number astronomers work with!

So, we came up with a new unit: the creatively named astronomical unit. It’s defined as the average distance between the Earth and the sun, abbreviated as AU.

But I’ll let you in on a secret. It’s not metric. And it’s not an SI unit, either. It’s more of a commonly accepted astronomical standard. Even in astronomy, though, it’s only useful for the shortest distances.

To measure the distance to the nearest star, we have to get even more creative…

Light-Year

A light-year is often mistaken for a unit of time. It is the distance that light travels in one year.

To put that another way: if your name is Bob, and you can travel 10 kilometers in 1 hour, then 10 kilometers could be known as a Bob-hour.

I have another post dedicated to explaining the light-year. But here’s the short story…

Light travels ridiculously fast–specifically, 299,792,458 meters per second. If you give it a whole year to travel, it’s gonna cover a massive distance. One light-year translates to 9,460,700,000,000 kilometers (or, for my fellow Americans, 5,878,600,000,000 miles).

Stars are quite a few light-years apart–even the nearest one, Proxima Centauri, is 4.3 light-years away. (Proxima Centauri is a companion star to Alpha Centauri, and currently closer to Earth.)

Light-years are abbreviated as ly.

But even light-years are not an SI unit, and the International Astronomical Union (IAU) advises against using them in scientific research.

Instead, the IAU recommends the use of parsecs. But we’ll get to those in a second…first, we need to cover degrees of arc!

Seconds/Minutes/Degrees of Arc

In observational astronomy, distances across the night sky are measured in degrees. For example, you might say that two stars in the night sky are separated by 3 degrees, or that an object such as the moon has an angular diameter of 0.52 degrees.

Here’s why:

You’re measuring the angle between two imaginary lines drawn between your eyes and the objects you’re measuring (or, in the case of angular diameter, the two opposite sides of the object’s disk).

These are not linear distances; they simply measure the separation between objects that we earthlings observe in the night sky.

Degrees of arc can also be broken down to minutes of arc and seconds of arc, or arcminutes and arcseconds. There are 60 arcminutes in a degree of arc, and 60 arcseconds in an arcminute.

Now we can talk about parsecs.

Parsecs

Hey, we’re back to Han Solo’s Kessel Run!

Parsecs are defined based on parallax. Parallax is the apparent change in position of an object when the observer changes position. You can try this yourself by holding up your finger in front of a background object such as a tree, and alternating which eye is open.

Your two eyes aren’t in the same place on your face. So they have slightly different perspectives. Think of them as two different observers. When you change which eye is open, you change the observer’s position.

Any object fairly close to you—in the case of this diagram, your finger—will appear to change position against its background.

The same goes for the stars. And when the change in the observer’s position (Earth’s position) is the diameter of its orbit, we can detect parallax among closer stars against the background of more distant stars.

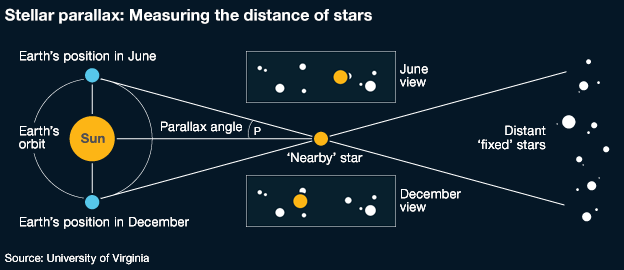
Now, see the “parallax angle” in this diagram?

When the parallax angle of a hypothetical star is 1 arcsecond, the distance to such a star is 1 parsec.

This distance comes out to 3.26 light-years. So, 1 parsec is 3.26 light-years long.

Keep in mind, though, that the nearest star is 4.3 light-years away–which is longer than a parsec. So there is no actual star at a distance of 1 parsec from the sun.

For even greater distances in astronomy–such as the distances between galaxies–we use the kiloparsec (kpc) or the megaparsec (Mpc). 1 kpc is 1000 pc; 1 Mpc is 1,000,000 pc.

Note that the parallax angle depends on Earth’s distance from the sun, or 1 AU: if the Earth were closer or farther, a parallax of 1 arcsecond would yield a different value for the length of the parsec.

Because a parsec is defined based on the astronomical unit, which is not an SI unit, a parsec is not an SI unit either. And neither are kiloparsecs or megaparsecs.

Parsecs are, however, the standard unit of distance among astronomers, preferred in academia over light-years.

Solar Units

And last but not least, we have the various solar units–solar mass, solar radii, and solar luminosities.

These units are all based on our sun.

Solar units are used to describe stars and galaxies alike. They all use the symbol ⊙, which represents the sun. Solar masses are represented as M_⊙, solar radii as R_⊙, and solar luminosities as L_⊙. 1 solar unit is always equivalent to the sun.

So, if a star has the same mass as the sun (is made up of the same amount of matter), it is 1 M_⊙. If it has 10 times the sun’s mass, then it is 10 M_⊙.

What if we wanted to measure the size of a star? Not the amount of stuff it’s made of, but the space it takes up?

We do this with solar radii (the plural for radius).

A radius is half of a diameter:

One solar radius–1 R_⊙–is the radius of the sun. A 2 R_⊙ star would have twice the sun’s radius (and twice the sun’s diameter).

Luminosity is a star’s total brightness, including all the radiation it emits across the electromagnetic spectrum. A 1 L_⊙ star would be exactly as bright as the sun. A 10 L_⊙ star would be 10 times as bright as the sun.

Like astronomical units, light-years, and parsecs, solar units are not SI units, but they are standard units in astronomy.

---

As you can see, most of the units astronomers use are not actually SI units. They have their own measurement system, standardized within the astronomical research community.

But astronomers will still choose kilometers over miles any day. In science, the metric system wins.