Imagine a time before galaxies existed, before the first stars had been born, before the most basic building blocks of matter–atoms–had formed.

This was mere moments after the Big Bang.

No one understands how matter and energy behave under the extreme conditions of the Big Bang itself. We can’t tell the story of the universe from exactly zero. But we can rewind the clock all the way back to the universe’s first one-millionth of a second.

So, what was the universe like back then?

This is a realm where Einstein’s famous equation, E=mc², comes into play.

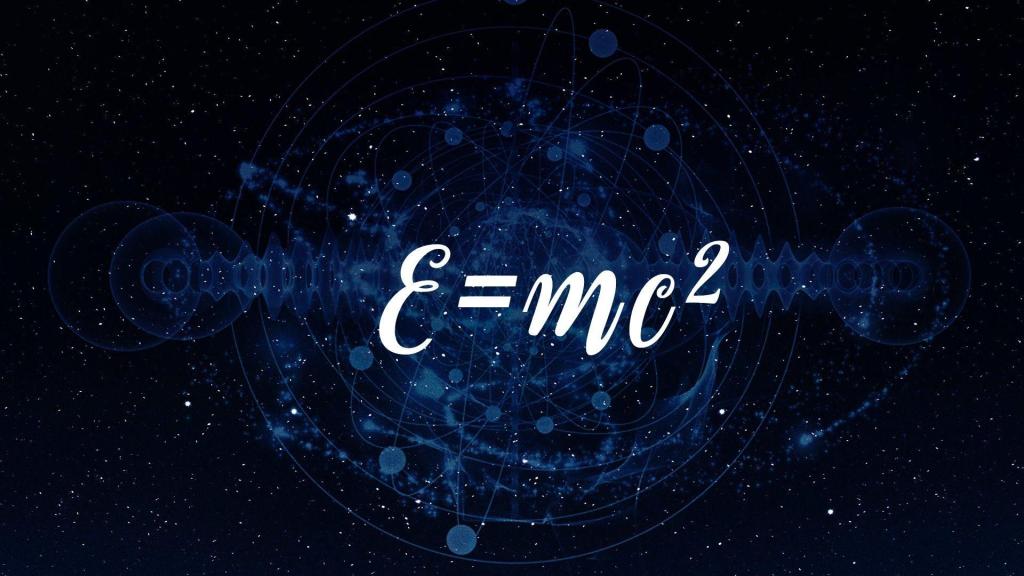
This is one of the world’s most powerful equations–because it relates matter to energy.

All you need to know for our purposes is that, according to E=mc², matter and energy are interchangeable.

Whaaaa?

Yeah, I know. That doesn’t sound like it makes much sense, does it?

It all has to do with one of the whackiest concepts that cosmology has to offer: antimatter.

Now what the heck is antimatter, you ask?

Don’t worry–I had the same exact question! The specifics and nitty-gritty of antimatter is beyond me at this point in my schooling, but the simplest answer is that it’s the “opposite” of ordinary matter.

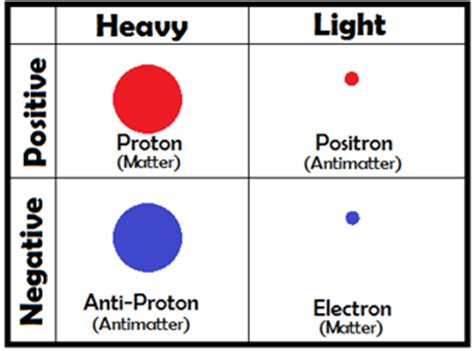
Think of the particles that make up an atom: protons, neutrons, and electrons. Each has a specific mass and electric charge:

• Protons are 1 amu (atomic mass unit); their charge is +1
• Electrons are 5.45 x 10^-4 amu (much smaller than a proton); their charge is -1
• Neutrons are 1 amu; their charge is 0

Now, where does antimatter come into this?

Protons are ordinary matter. Their antimatter counterpart is the antiproton, a particle that has the same mass as a proton and an opposite charge of -1. (Note that despite having the same charge as an electron, antiprotons are not electrons because they have the same mass as a proton.)

Electrons’ antimatter counterpart is an antielectron or a positron–alternate names for the same particle. Positrons have an opposite charge (+1), but the same mass as an electron. (Note, again, that positrons have the charge of a proton but they are not protons–their mass is the same as an electron.)

There are also antineutrons, the antimatter counterpart of neutrons. I’m honestly not sure what makes them “opposite,” since neutrons have no charge. But as I understand it, they have the same mass as a neutron.

(What are neutrinos, you ask? More here.)

Now, here’s the key.

When a particle and its antiparticle meet, they annihilate each other.

This annihilation produces two gamma rays–a high-energy form of electromagnetic radiation.

And there you have it: E=mc².

Or, at least, we have it in one direction. See how matter just converted into energy? Two particles of matter–one ordinary matter, one antimatter–collided, were annihilated, converted their mass into gamma rays.

And energy can convert to matter, too.

High-energy photons (particles of light) can convert into a pair of particles: specifically, a matter-antimatter pair.

Because matter and energy are interchangeable, cosmologists describe photons as having a temperature, as if they were actually matter. They mean that the photons have the same spectrum as blackbody radiation emitted from an object of that temperature.

We can even describe radiation–that is, light–as having density, as if it were matter. We simply use E=mc² to relate energy to matter and express an amount of radiation energy per volume as if it were matter of a certain density.

Now, back to the early universe.

In the universe’s first one-millionth of a second, it was filled with high-energy photons with temperatures of 20 trillion K (Kelvins). That’s a lot of energy–so we’re talking gamma rays.

Hey, remember what we were just saying about high-energy photons being able to convert into a matter-antimatter pair of particles?

Yup. Exactly.

This radiation was also very “dense”–at 5 x 10²⁰ kg/m³–over a thousand times the density of an atomic nucleus. So when gamma rays converted to matter-antimatter pairs, these particles were packed pretty close together.

The result? Matter-antimatter pairs wouldn’t stick around. Gamma rays would barely just convert into particles before the particles would collide, annihilate, and convert back to gamma rays.

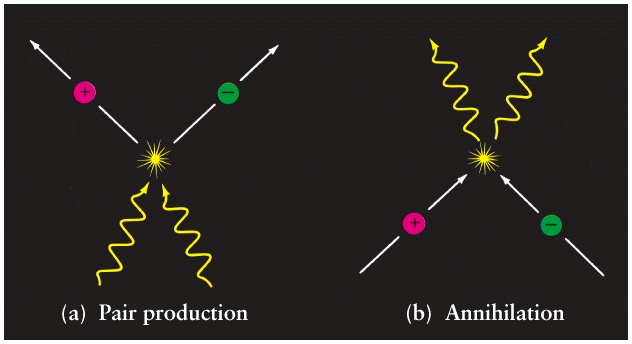
So, this early universe was a soup of energy, flickering between particles and photons and back again.

But remember, it’s only been one-millionth of a second since the beginning of time.

During this fraction of a second, the universe continued to expand. This would have reduced the temperature of the radiation and, consequently, the energy of the photons. By the time 10 millionths of a second had passed, the temperature would’ve dropped from 20 trillion K to “only” about 2 trillion K.

According to E=mc², mass matters–and the more massive the particle, the more energy it takes for photons to convert to the particle.

So, at this point, photons could no longer produce proton-antiproton pairs or neutron-antineutron pairs.

But the universe was still dense, particles crammed close together. The existing particles would’ve combined with their antiparticles, annihilated one another, and converted their mass to photons–and stayed that way.

Electrons and positrons are about 1800 times less massive than protons and neutrons, so they still remained within the universe’s energy budget…at least for another 60 seconds. Then, they too would’ve combined and converted to photons for good.

Which leads to one of the most vexing questions in cosmology…

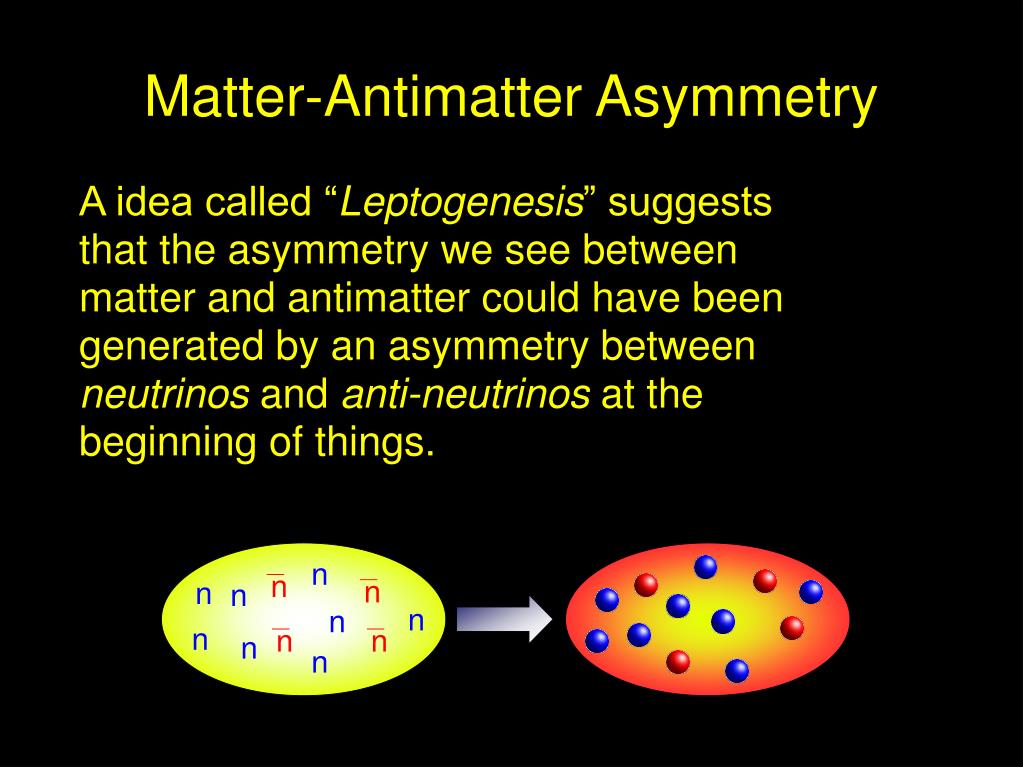
Why is there any matter in the universe?

All particles of matter–and their antimatter counterparts–should have been annihilated. Only radiation should have remained.

But for some reason we haven’t figured out, the Big Bang produced a little bit more matter than antimatter. For every billion matter-antimatter pairs, one particle of matter survived with no antiparticle to annihilate it.

And here’s the craziest thing…

It’s only been 1 minute.

All the matter in the universe–everything that makes up you and me, your dog, your house, your computer, our planet, our galaxy–was produced in that first minute of the universe’s existence.

Next up, we’ll explore the formation of the first atomic nuclei…and a major piece of evidence that gives cosmologists confidence in the big bang theory.